Tips for Integration by Parts

Hi y’all.

Here are some tips for tackling a few types of integrals. I’ll be focusing on integrals that you solve using Integration By Parts (IBP).

Here’s the formula for IBP:

$\int{u\frac{dv}{dx}}=uv-\int{v\frac{du}{dx}}$

This formula tells you that you have to differentiate one term (the term that you set as $v$) and you have to integrate one term (the term that you set as $\frac{dv}{dx}$). So when you apply this formula, have a clear idea of how to integrate/differentiate the 2 terms appropriately. IBP questions at their core are just figuring out which terms should be set as $u$ and which should be set as $\frac{dv}{dx}$.

First up: Integrals containing both $x^n$ and $e^x$, i.e. the integral of $x^ne^x$ .

Here you’d aim to repeatedly differentiate the $x^n$ term till you reach $x^1$ (that is, till you’re left with $x$). You’d set $x^n$ as $u$ in the initial integral. Once you’ve done that, use IBP again. Set $x^{n-1}$ as $u$ again to differentiate it again and so on…

In the process, you’ll be repeatedly integrating $e^x$. But the nice thing about $e^x$ is that its integral is itself, so you don’t have to worry about that. Once you’ve gotten to $x$, just clean it up.

An example:

$\int x^2e^xdx$

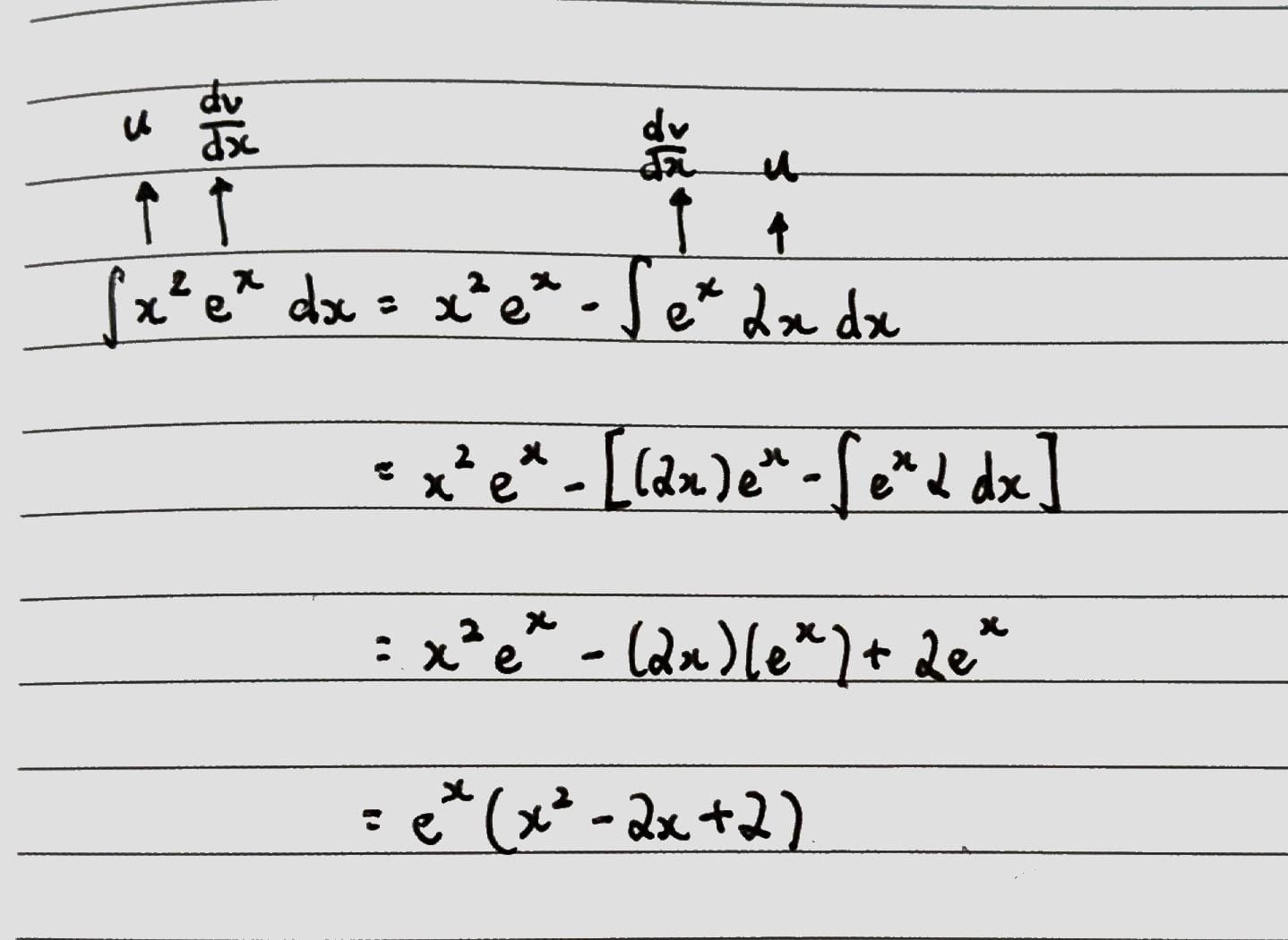
In a similiar vein, the 2nd type of integrals we’re looking at contain $sin(x)$ or $cos(x)$, and $e^x$. (e.g. $e^xsin(x)$). Repeatedly set the trigonometric function as $u$ to differentiate it. Differentiating it twice will reform the initial integral. Then manipulate the equation to make the initial integral the subject of the formula.

2 examples:

$\int e^xsin(x)dx$

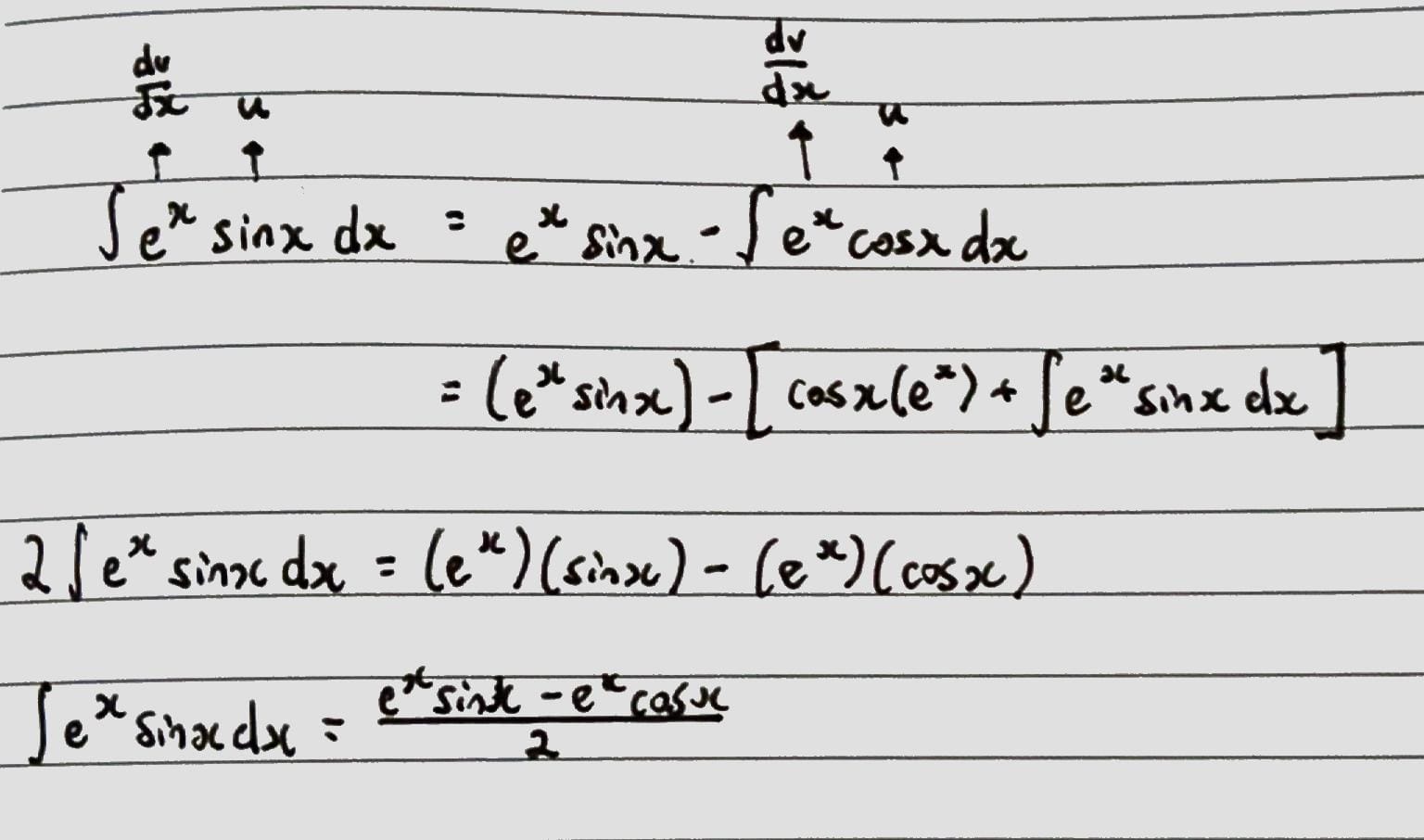
$\int e^{3x}cos(4x)dx$

The key concept for the 2nd type of integral is to flipflop your terms between $sin(x)$ and $cos(x)$, which eventually allows you to reform the initial integral. You could also flipflop your trigonometric functions by repeatedly integrating them, but I’d advise against that since:

1. You’re probably more familiar with differentiation
2. Integrating the trigonometric functions makes it messier

(Why not try the above 2 examples for some practice?) Do also note that the sneaky folks over at the Math Department get their kicks from tricking students.
Consider this:

$\int 2x^3e^{x^2}dx$

It seems like the 2 terms that you’ll be dealing with are $2x^3$ and $e^{x^2}$, but you actually need to separate it like this:

Keep your wits about yourself.
“We making moves and strides, grooves and vibes” - Lil Wayne